우리는 최대 혹은 최소를 기준으로 Queue에서 빼내오기 위해서 PriorityQueue(우선순위 큐)를 사용한다.
Java에서는 PriorityQueue를 구현하기 위해서 Heap(힙)을 사용하였다.
왜 Heap을 사용하였을까? 그리고 Heap이 무엇일까?
먼저 Heap을 이해하기 위해서는 완전 이진 트리(Complete Binary Tree)에 대해서 알고 있어야한다.
완전 이진 트리는 이진 트리 중 모든 부모 노드의 자식이 왼쪽부터 채워져있어야 한다.
이진트리

자 그럼 Heap에 대해 알아보자.
Heap
Heap은 트리 개념을 사용한 자료구조인데 만약 완전 이진 트리라면 힙 개념을 사용할 수 있다.
Heap은 최대 힙(Max Heap)과 최소 힙(Min Heap)으로 두 가지로 나눌 수있다.
MaxHeap을 이해하면 Min Heap은 자연스럽게 이해가 가능하기 때문에 Max Heap에 대해서만 자세하게 설명을 해보겠다.
최대 힙(Max Heap)
heapify
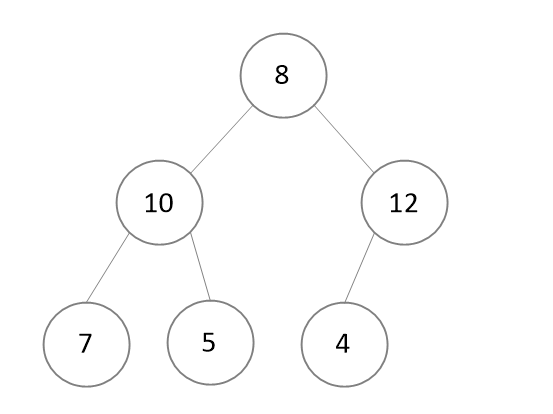
완전 이진 트리이면서 모든 부모노드가 자식노드보다 큰 경우를 말한다.

위와 같이 최대 힙 구조에서 루트 노드 12가 가장 높은 우선순위를 가지며
그 다음부터는 왼쪽부터 오른쪽 순서로 10, 8, 7, 5, 4 순으로 우선순위를 가지게 되어
숫자가 높은 것을 기준으로 우선순위를 갖게 되는 것이 Max Heap이고,
이러한 '기준을 정해서' 우선순위가 높은 것을 순서대로 빼내는 것이 Heap이다.
그렇다면 Max Heap은 어떻게 만들고, 어떻게 꺼내는지에 대한 과정을 알아보겠다.

위와 같이 완전 이진트리가 있다고 하자.
최대 힙은 가장 작은 단위의 트리의 루트 노드부터 탐색하여 만약 루트노드가 자식을 가지고 있으며, 자식이 루트노드보다 크다면 루트노드와 바꿔주는 작업을 반복적으로 수행하여 만들 수 있고
이 작업을 하는 것이 heapify다.
heapify의 목적은 트리의 모든SubTree에 대해 Heap 구조를 만족시키게 하여, 전체적으로 Heap 구조를 만족시키게 하는 것이다.
heapify의 과정을 그림으로 알아보자.

여기서 가장 작은 Sub Tree는 7, 5, 4이다.
완전 이진트리는 왼쪽부터 자식을 채워넣기 때문에 heapify는 오른쪽에서부터 수행한다.

빨간색 친 네모 부분을 Sub Tree로 본다면 4는 루트 노드가 된다.
루트 노드의 자식이 없으므로Max Heap 구조를 만족시켰다고 볼 수 있으며 이후의 7, 5에 대해서도 같은 방식으로 넘어갈 수 있다.
(구현에서는 최대 깊이에 대해서는 수행하지 않는다. 어차피 자식이 없기 때문에)

그 다음으로 처음 자식을 갖게 되는 Sub Tree의 루트노드는 3이다.
자식 4가 부모 3보다 크기때문에 부모 노드와 바꿔준다.

이렇게 부모 노드와 자식 노드가 바뀌는 Swap 과정이 한 번 일어나게 되면, 바뀌어진 자식 노드에 대해 다시 heapify를 수행하고, Max Heap 구조를 만족시킬 때까지 반복한다.

3의 자식은 없으므로 Max Heap구조를 만족시켰기 때문에 다음으로 넘어간다.

그 다음으로 볼 것은 루트 노드가 10인 Sub Tree인데, 이 Sub Tree는 Max Heap 구조를 만족시키므로 넘어간다.

마지막 으로 볼 루트 노드가 2인 Sub Tree이다. 이 Sub Tree는 Max Heap 구조를 만족시키지 않는다.
부모 노드 2보다 큰 자식 노드 10과 4가 존재하기 때문이다.
Max Heap 에서의 heapify는 자식 노드 중, 가장 큰 것과 swap이 일어나고,

바뀌어진 자식 노드에 대해 반복적으로 heapify를 수행하면 다음과 같다.


이렇게 heapify 과정을 통해 모든 Sub Tree에 대해 Max Heap 구조를 만족시키게 하여 전체 Tree를 Max Heap 구조로 만들었다.
그럼 이제 Max Heap 구조가 되었으니 빼내는 연산도 알아보자.
Max Heap에서 pop연산을 하게 되면 가장 큰 값(루트 노드)이 나오게 된다.
하지만 우리는 Heap구조를 유지해야하기 때문에 루트 노드를 삭제할 수는 없기 때문에
1. 우선 순위가 가장 높은 노드(루트)와 가장 낮은 노드를 swap
2. heapify 수행
3. 1, 2 반복
위와 같은 과정을 통해서 모든 노드를 빼낸다.
그림으로 보면 다음과 같다.





이렇게 pop을 한 번 하면 노랗게 칠해진 노드를 제외하면 Max Heap 구조를 유지할 수 있다.
이러한 방식으로 그 다음 루트 노드인 7을 제거한다면 다음과 같다.




이런 식으로 우선수위가 높은 것을 맨 뒤 노드와 swap하고 heapify를 수행한다면, 루트 노드에는 그 다음 우선순위인 노드가 들어가게 되며

결국 위와 같은 상태를 볼 수 있다.
여기까지가 Max Heap이었다.
그런데 잠깐! 자세히 보니 오름차순 정렬이 되어있다.
그렇다. Max Heap을 사용한다면 노드들을 오름차순으로 정렬을 할 수 있고, 이것이 HeapSort(힙 정렬)이다.
반대로 Min Heap을 이용하여 내림차순으로 정렬할 수도 있다는 말이 된다.
HeapSort관련해서는 아래 링크 참고
[알고리즘] 힙 정렬(heap sort)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
최소 힙(Min Heap)
Max Heap과 99% 비슷하다.
다른 점이 있다면 heapify의 비교 조건이다.
heapify 과정 중 swap하는 조건을 부모노드가 자식 노드보다 클 때 swap한다고만 바꿔주면 된다.
힙 정렬(heap sort) 알고리즘의 특징
장점
시간 복잡도가 좋은편
힙 정렬이 가장 유용한 경우는 전체 자료를 정렬하는 것이 아니라 가장 큰 값 몇개만 필요할 때 이다.
HeapSort(힙 정렬)
HeapSort의 시간 복잡도는 힙 트리의 높이가 logN이므로 N개의 요소에 대해 연산을 할 경우 NlogN이 걸린다.
최악, 최선, 평균에 대해 동일한 시간 복잡도를 가진다는게 특징이다. ( 정렬 상태에 따라 실질적인 시간은 다르다)
최악 : O(NlogN)
최선 : O(NlogN)
평균 : O(NlogN)
힙 정렬이 유용한 경우는 전체 자료를 정렬하기 보다는 가장 큰 값 또는 작은 값 몇 개만 필요할 때이기 때문에,
Java에서는 PriorityQueue에서 사용되며
Java의 Aarrays는 InsertSort(삽입정렬)과 QuickSort(퀵 정렬)을 이용한Dual-pivot QuickSort를,
Collections는 InsertSort(삽입정렬)과 MergeSort(합병 정렬)을 이용한 TimSort를 채택했다.
Arrays에서 퀵정렬을 사용하는 이유는 기본 자료형이기 때문에 unStable한 정렬이어도 상관 없기 때문이고,
Collections에서 합병정렬을 사용하는 이유는 Element 자료형이기 때문에 순서가 보장되어야 하기 때문에 Stable 정렬인 MergeSort를 사용한다.
이러한 이유로 퀵 정렬과 힙 정렬의 비슷한 시간 복잡도임에도 불구하고 Java에서는 힙 정렬을 사용하지 않는 것으로 알고있다.
+) 퀵 정렬은 분할 정복기법으로 부분적으로 정렬을 하기 때문에, 중간 과정에서 다른 정렬 기법을 섞어 쓸 수 있어 유연하지만 힙 정렬은 그렇지 않기 때문에 힙정렬을 채택하지 않은 걸 수도...